囚人のジレンマという話をご存じでしょうか？
この話の登場人物は2人の囚人で、取調官から罪を自白するか、黙秘するかの選択肢を迫られます。
罪を自白せずに刑期を短くするという、一番理想とする選択肢が提示されます。
ですが、合理的に考えるとその選択肢を選べないようになっていて、囚人2人は罪を自白させられてしまいます。
なぜこのような選択になってしまうのか？
パラバース博士自分ならどう選択するかも考えながら読んでみてください。
囚人のジレンマとは？
囚人のジレンマとは、1950年に数学者のアルバート・タッカーが考案した思考実験です。
お互いが協力するほうが絶対に良い結果になることが分かっている状況。
その状況下でも、協力しない側が利益を得られる状況では互いに協力しなくなるというジレンマです。
内容は以下のようなものです。
共同で犯罪を犯したと思われる囚人Aと囚人Bがいる。
取調官は、囚人A、Bにおのおの別の場所で、次のような話を持ち掛けた。
「2人にかけられている容疑の刑期は、5年だ。」
「ただしこのまま2人とも黙秘を続けていれば証拠不十分となる。刑期は減刑されて懲役2年になる。」
「2人とも罪を自白すれば、刑期は変わらず5年だ。」
「１人だけが自白すれば、自白した方は釈放する。黙秘を続けた相方の刑期は10年にする。」
お互い、相談は出来ない。さて、自白するべきか？
囚人のジレンマの問題点
パラバース博士この話の問題点は、2人の囚人A・Bはそれぞれ自白するべきか黙秘するべきかということです。
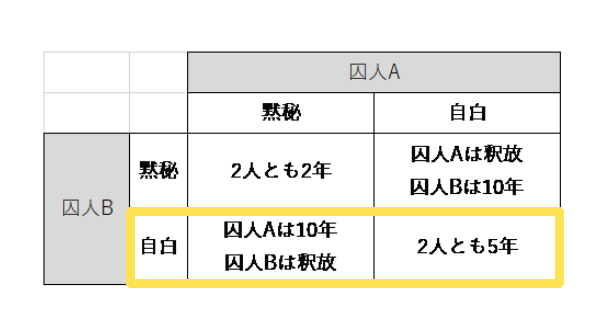
パラバース博士囚人2人の選択肢を表にまとめると、このようになります。
この表で考えると、2人とも黙秘をした方がいいので、どちらの囚人も自白することはないんじゃないですか？
パラバース博士全体としての利益を考えるとそうなりますね。ただし、片方だけの立場で考えてみるとそう一筋縄ではいかないことが分かります。
囚人Aの立場で考えた時
囚人Aの立場に立って、囚人Bが黙秘、自白したときのそれぞれの結果を考えてみましょう。
囚人Bが黙秘したとき
- パターン①：囚人Aも黙秘 → 2人の刑期は2年
- パターン②：囚人Aは自白 → 囚人Bのみ刑期10年(囚人Aの刑期は0年)
よって、囚人Bが黙秘したときは囚人Aは自白した方が得。
囚人Bが自白したとき
- パターン①：囚人Aも自白 → 2人の刑期は5年
- パターン②：囚人Aは黙秘 → 囚人Aのみ刑期10年(囚人Bの刑期は0年)
よって、囚人Bが自白したときも囚人Aは自白した方が得。
パラバース博士囚人Bが黙秘しようが自白しようが、囚人Aは自白した方が得になるという結果になります。
あれっ、さっきの「2人とも黙秘した方がいい」とは違う結論になってしまいましたね…
パラバース博士はい、このように、合理的な選択肢をとったことで、最適な結果にならなくなってしまいます。これが、この話の“ジレンマ”たる所以です。
ナッシュ均衡とパレート最適
この問題には、次の3つが関係しています。
- 「最適反応」
- 「ナッシュ均衡」
- 「パレート最適」
これらの用語はゲーム理論の他に経済学でも使われるのですが、この記事ではゲーム理論という分野に限って説明をします。
最適反応
他のゲーム参加者の戦略を考慮したうえで、利益が最大となる選択をする戦略。
ナッシュ均衡
ゲーム参加者全員の最適反応の組み合わせ。
パレート最適
ゲーム参加者全員の利益が最大となっている状態。
パラバース博士ゲーム参加者全員の利益が最大となるパレート最適はどのような選択でしょうか？
2人とも「黙秘する」です。
パラバース博士はい。では、囚人Aの最適反応はなんでしょうか？
囚人Bがどちらの選択をするか分からないから、「自白する」でしたよね？
パラバース博士そうです。では囚人Aと囚人Bの最適反応を組み合わせた、ナッシュ均衡はどうなりますか？
2人とも「自白する」になります…
ナッシュ均衡の選択とパレート最適の選択は、同じではないんですね。
このように、ゲーム理論では、ナッシュ均衡が必ずしもパレート最適とはならないことがあります。
そのために、ジレンマのようなことが起こってしまうのです。
期待値というもう一つの考え方
パラバース博士この話の、もう一つの考え方を解説しましょう。
数学には、期待値という考え方があります。
宝くじを例に挙げてみましょう。
くじは全部で1000枚あるとします。
当たりが出た時の金額と、当たりの出る確率は、次の通りです。
- 1等10万円 3/1000
- 2等1万円 20/1000
- 3等5千円 50/1000
- 4等1000円 300/1000
- 5等100円 1～4等以外の残りくじ全て
計算すると、このようになります。(計算方法の説明は省略しています)
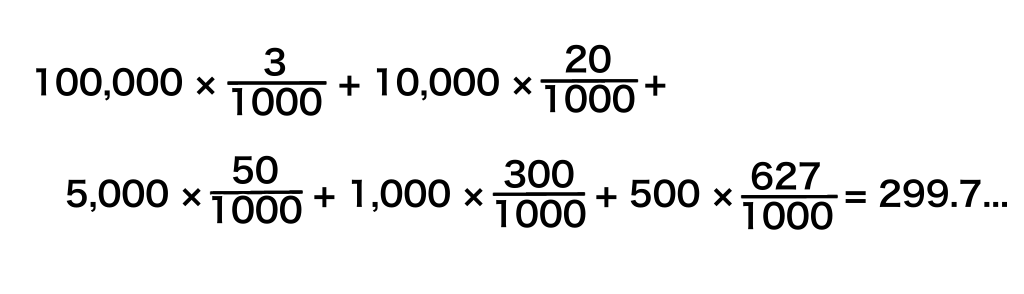
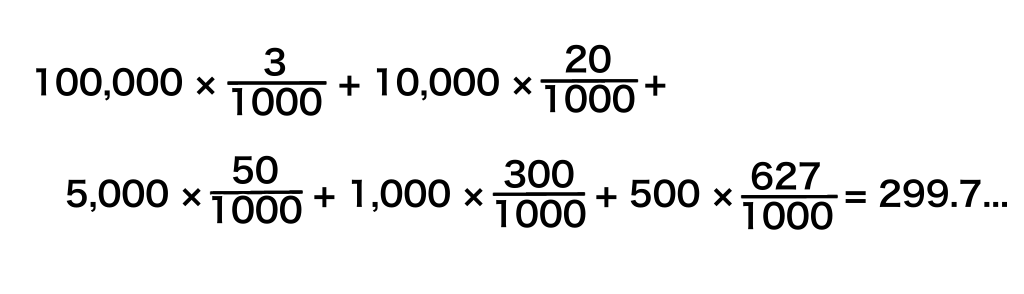
つまり、この宝くじを買ってを当たる金額の期待値は299円。
約300円ということになります。
つまり、この宝くじ一口の値段が300円以下であれば得をする可能性の方が高く、300円以上であれば損をする可能性の方が高い、ということになります。
パラバース博士この期待値の計算を使って、囚人のジレンマについて考えてみましょう。
期待値を計算するための値と刑期を、次にように対応させます。
- 刑期がなく釈放された時を0
- 刑期が2年の時を-2
- 刑期が5年の時を-5
- 刑期が10年の時を-10
数値はなぜマイナスなのですか？
パラバース博士刑期が長くなるほど、自分にとって損になるという意味で、マイナスにしています。
自分が自白したとき
相手が自白する可能性と、黙秘する可能性が1/2ずつだとします。
このとき、全体の期待値はこのようになります。
0 ×1/2 + (-5)×1/2 = -2.5
つまり自分が自白したときの期待値は、刑期2.5年です。
自分が黙秘したとき
同じく相手が自白する可能性と、黙秘する可能性が1/2ずつだとすると、全体の期待値はこのようになります。
-2 ×1/2 + (-10)×1/2 = -7
自分が黙秘したときの期待値は、刑期7年です。
黙秘したときの方が、刑期の長さの期待値が大きくなってしまうのです。
よって、期待値的にも「自白したほうがいい」となります。
囚人の「ジレンマ」と言われる理由？
この話の面白いところは、囚人A、囚人Bの2人ともが合理的な選択をしても、それが最適解ではないというところ。
そして、もう一人が裏切るか？などの疑いによる選択のブレを除いても、合理的な選択は「自白する」になるということです。
確かに、理想はお互い黙秘することだけれど、相手が裏切るかもしれないと考えたら、自分は自白したほうが損しないので自白するかもしれません…でも、理論的にも自白することが一番合理的なんですね
まとめ
合理的って何なんだろう？と思わされてしまいました…
パラバース博士この話では合理的な選択に注目して紹介しましたが、もし仲間を信頼しているならば黙秘すればいいのです。
もし、「合理的」ということだけを考えるのであれば、世の中の宝くじやパチンコなどの娯楽もちろん、嗜好品の多くは成り立たないかもしれません。
パラバース博士合理的でなくても、期待値が低くても、期待したくなってしまうのは人間のサガです。
「合理的か」にこだわりすぎるのも、よくないかもしれませんね。良いところでバランスをとって楽しむのが、大事なのですね。
コメント