モンティ・ホール問題をご存じでしょうか？
確率論の問題なのですが、数学者をはじめとする数学のプロも、この問題にことごとく翻弄されたことから、数学史上最も議論を巻き起こしたともいわれています。
この問題の何が、そこまで人々を惑わせたのか？
パラバース博士この記事では、数学者たちをも惑わせたこの問題を、誰でも理解できるように紹介・解説します。
モンティ・ホール問題とは
モンティ・ホールが司会者を務める、アメリカのゲームショー番組のなかで行われたゲームからきている確率論の問題です。
直感と異なる結果になることから、モンティ・ホールのジレンマ、モンティ・ホールのパラドックスともいわれます。
プレイヤーの前に、閉じた3つのドアがある。
1つの扉の向こうには当たりの新車が、2つの扉の向こうにははずれを意味するヤギがいて、あたりの扉を当てれば新車がもらえる。
プレイヤーが一つのドアを選択した後、司会者のモンティが残りのドアのうちヤギのいるドアを開けてヤギを見せる。
ここでプレイヤーは、いま選択しているドアを、もう一つのドアに変えても良いといわれる。
ここでプレイヤーはドアを変更するべきだろうか？
パラバース博士さて、どう思いますか？
あたりの確率は1/3ですよね。はずれの扉が分かったところで、扉を変えても変えなくても同じなんじゃないでしょうか。
パラバース博士直感的にはそう思いますよね。当時の人も、大半がそう思っていました。ですが、これに真反対の意見を唱える人が現れたのです。
史上最もIQの高い女性からの指摘
史上最もIQが高いとギネス認定されているマリリン・ボス・サヴァントが雑誌の中で「扉を変えたほうがあたりの確率が2倍になる」と指摘しました。
そして、マリリンの主張のほうが正しかったことがのちに分かります。
当時、マリリンの主張はなかなか受け入れられず、マリリンの主張に反論する1万通以上の投書が殺到しました。
その中には、1000人近い博士号保持者からの投書もあったようです。
なぜ、数学のプロであるはずの数学者の間ですら意見が分かれてしまったのでしょうか。
パラバース博士これは、前提条件が共有がされていなかったからです。
共有されていなかった前提条件とは、次の二つです。
・モンティは、プレイヤーの選択後必ず1つの扉を開ける
・モンティはあたりの扉を知っていて、必ず、はずれの扉を開ける
この条件のもとに確率を計算すると、扉を変えたほうがあたる確率は2倍になります。
そしてマリリンは暗黙の了解として、この2つの条件を使って答えを出していたのです。
ちなみに直感的に確率が変わらないように思えるのは、「モンティがランダムに扉を開けているように思える」からです。
実際モンティがランダムに扉を開けていた場合は、扉を変えても変えなくても確率は変わりません。
モンティ・ホール問題で扉を変えたほうがいいのはなぜ？
ちょっと納得できません…モンティがあたりの扉を知っていようがいまいが、確率は1/3じゃないんでしょうか…
パラバース博士これから詳しく解説します。
扉を変える場合
扉を変える場合を考えます。
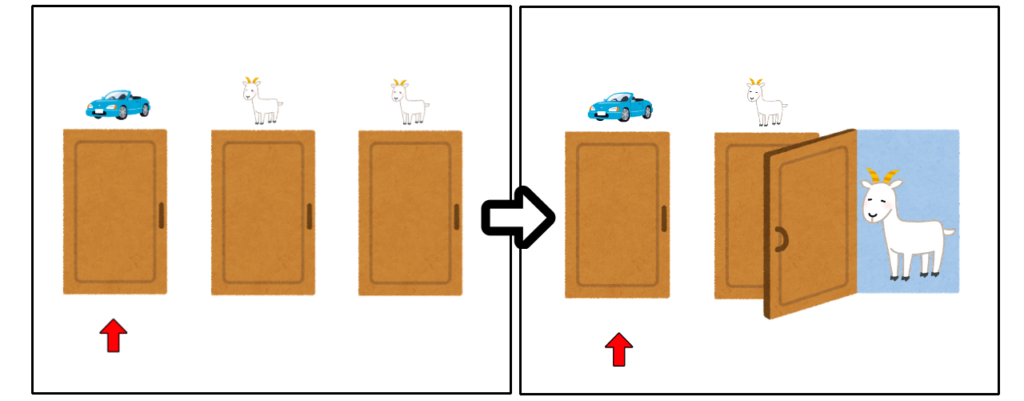
まず、あたりの扉を最初に選んだとします。
モンティは、残りのはずれの扉のうちどちらかをランダムで選び、開けます。
この後、扉を変えると、最終的に残ったはずれの扉を選ぶことになります。
あたりだった選択がはずれに変わるということです。
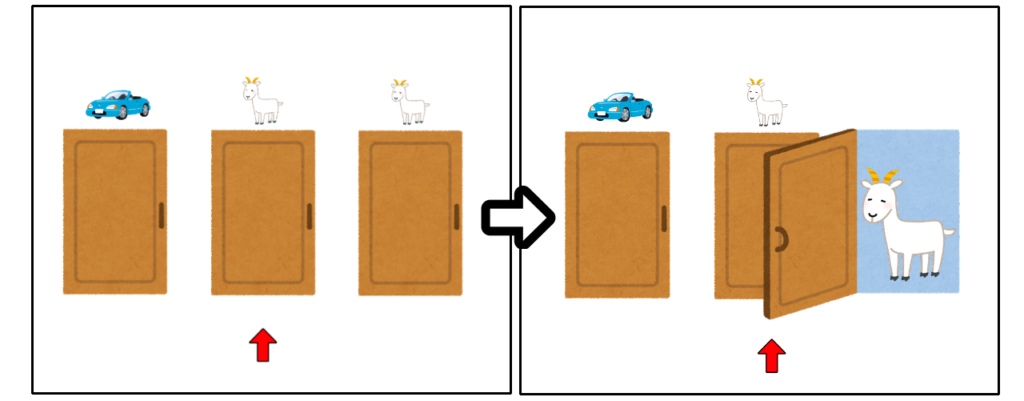
次に、はずれの扉を最初に選んだとします。
モンティは、残りのあたりの扉とはずれの扉のうち、必ずはずれの扉を開きます。
この後、扉を変えると、最終的に残ったあたりの扉を選ぶことになります。
はずれだった選択があたりに変わるということです。
すべてのパターンを考えると、次のようになります。
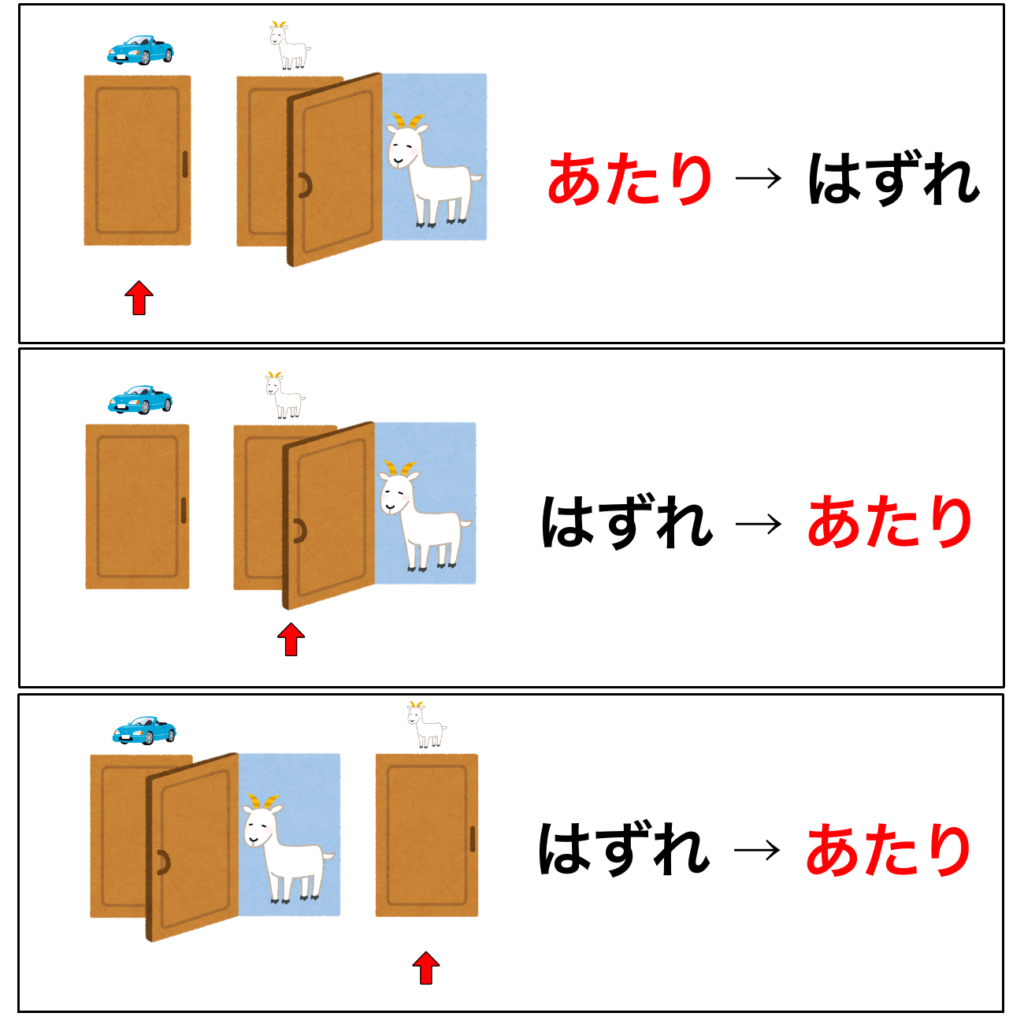
扉を変えた場合、最終的に選ぶ扉があたりになるのが3パターンのうち2パターン。
はずれになるのが3パターンのうち1パターンになります。
つまり、あたりを選ぶ確率が2/3、はずれを選ぶ確率が1/3となります。
ここで、扉を変えない場合のパターンと比べてみましょう。
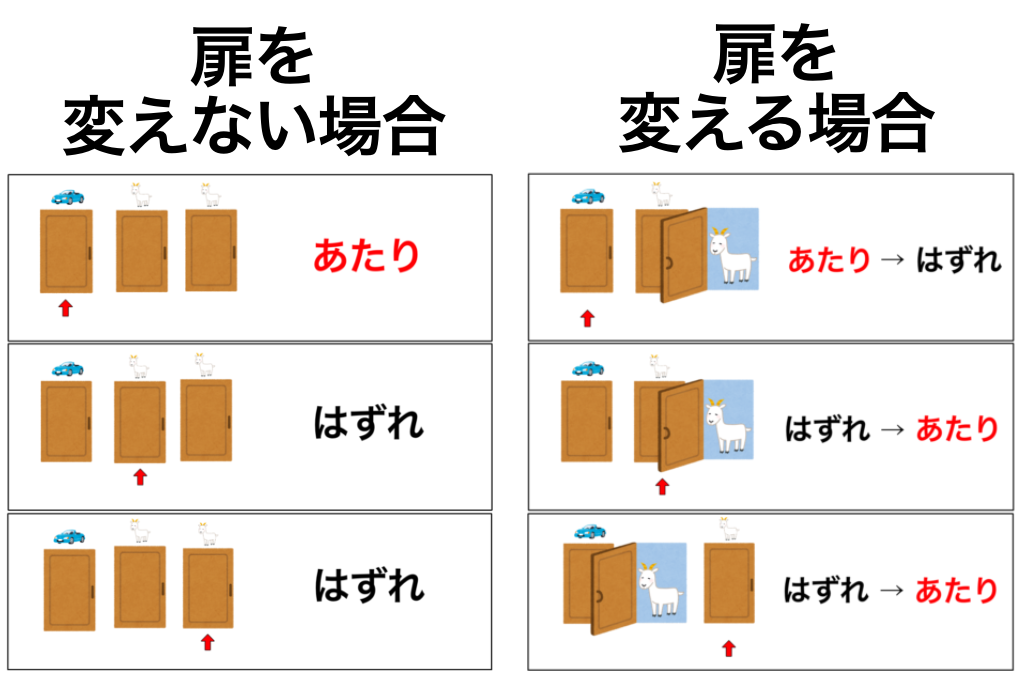
扉を変えない時のあたりの確率は1/3。
扉を変えた時のあたりの確率は2/3。
このように、扉を変えない時よりも、扉を変えた時の方があたりの確率が2倍になるのです。
なるほど！モンティがあたりの扉を知っていて、“必ずはずれの扉を開ける”というところがポイントなんですね！
パラバース博士その通りです！
まとめ
モンティ・ホール問題を知ると、直感と異なる結果になることが、人間にとってどれだけ受け入れ難いかが良く分かります。
パラバース博士もしかしたら私たちも日常生活で、思い込みや直感に囚われて騙されているかもしれません。
そう考えると怖いですね…知らないうちに騙されないように、日々考えることを辞めないようにしたいです！
コメント