「この世にいるカラスが黒いことを証明して下さい」と言われたら？
世界中にいるカラスを1羽1羽調べる事は当然不可能ですが、
カラスを1羽も調べずに証明できる方法があるのです。
その方法は「ヘンペルのカラス」と呼ばれています。
カラスを調べずに、どうやって「カラスが黒い」ことを証明するのか？
パラバース博士今回は「ヘンペルのカラス」の謎を詳しく解説します
パラバース博士数学が苦手な方でも、イラストを使って分かりやすく解説するのでご安心下さい。
「ヘンペルのカラス」とは？
ヘンペルのカラスは、ドイツの科学哲学者であるカール・ヘンペルが1940年代に提起しました。
「全てのカラスは黒い」を証明する方法を示したもので、対偶論法(たいぐうろんぽう)を使えば「全てのカラスが黒い」ことをカラスを1羽も調べずに証明できると示したのです。
ヘンペルの主張は以下の通り。
「全てのカラスが黒い」ことを証明するためには「全ての黒くないものはカラスではない」ことを証明すればよい。
一見矛盾しているように感じることから、カラスのパラドックスとも呼ばれます。
(厳密にはパラドックスではない)
対偶論法って何ですか？ちょっとよく分からないです💦
パラバース博士これから詳しく説明します。
対偶論法(たいぐうろんぽう)とは？
対偶論法(たいぐうろんぽう)とは、数学的な証明方法の1つです。
数学には“命題”という概念があり「正しい&正しくない」を決める事柄です。
「ＡならばＢである」のような表現で使われることが多く、これが正しいときは“正”、正しくないときは“偽”と呼びます。
数学の命題には以下の様な関係があります。
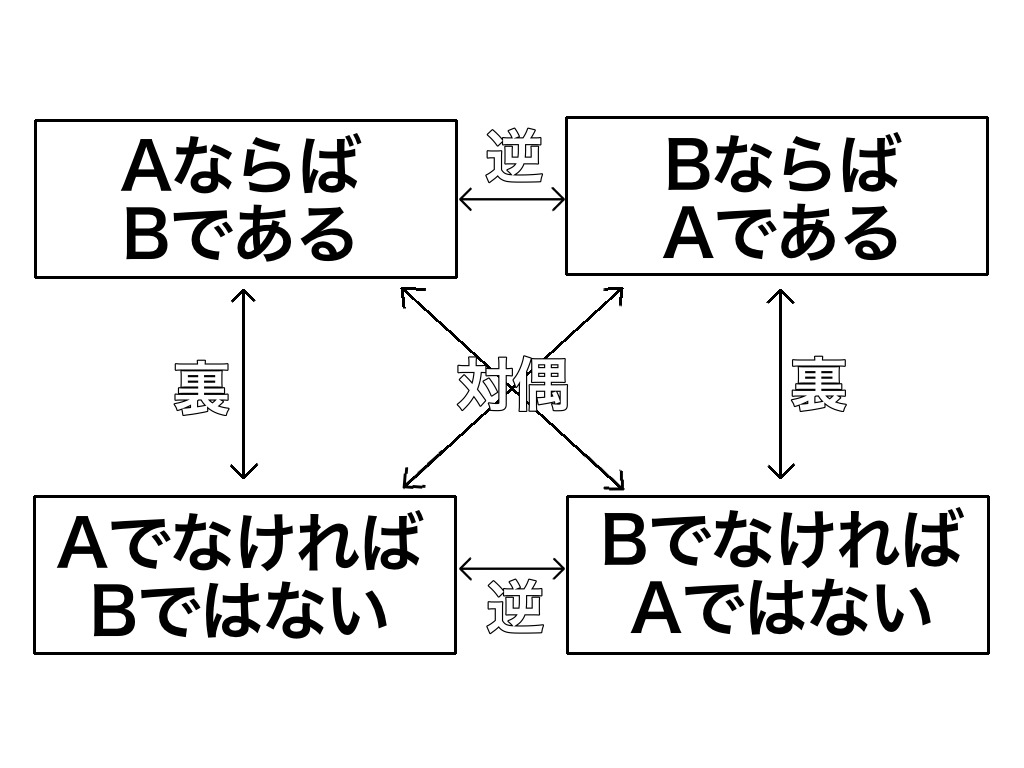
↑ある命題の“逆”と“裏”は正と偽が反対に、“対偶”では正か偽が同じになると言うこと。
パラバース博士例を挙げてみましょう。「人間なら生き物である」は正ですか？偽ですか？
これは正しいので「正」です。
パラバース博士正解です。では続いて「生き物なら人間である」これはどうでしょうか？
これは間違っているので「偽」です。人間以外にも、犬&猫、虫も生き物ですから。
パラバース博士正解です！では「生き物でなければ人間ではない」これはどうでしょうか？
「人間＝生き物」なので「生き物でない＝人間はありえない」ですよね…？なので「正」ですか？
パラバース博士正解です！
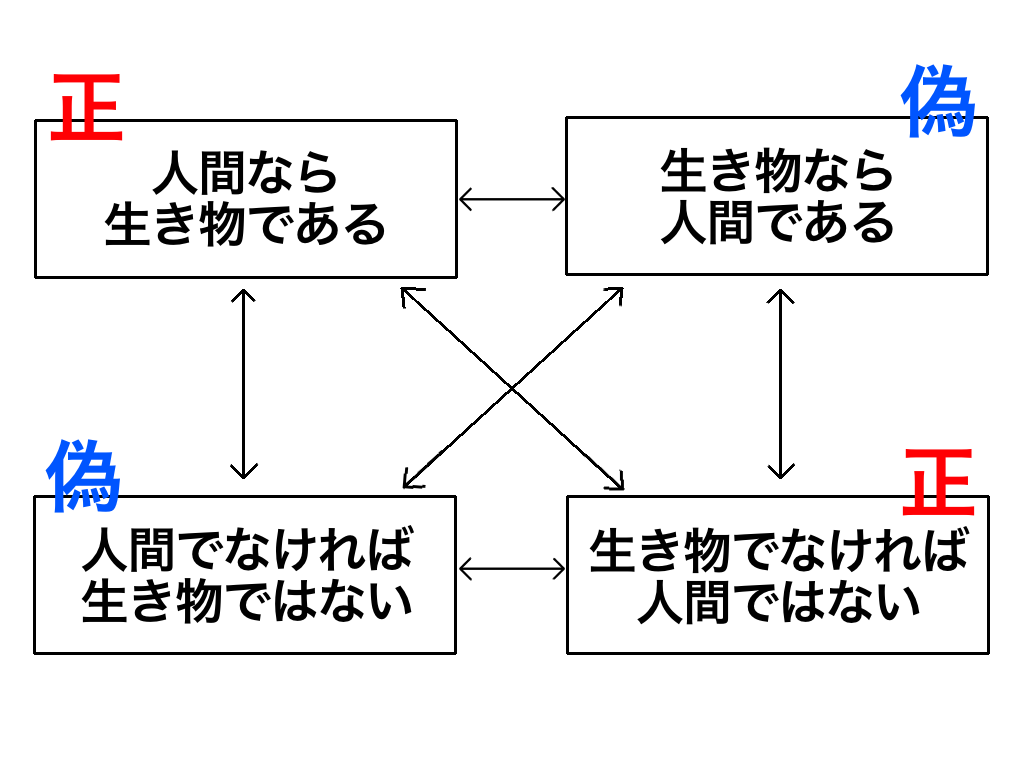
このように、命題には必ずこのような関係が成り立ちます。
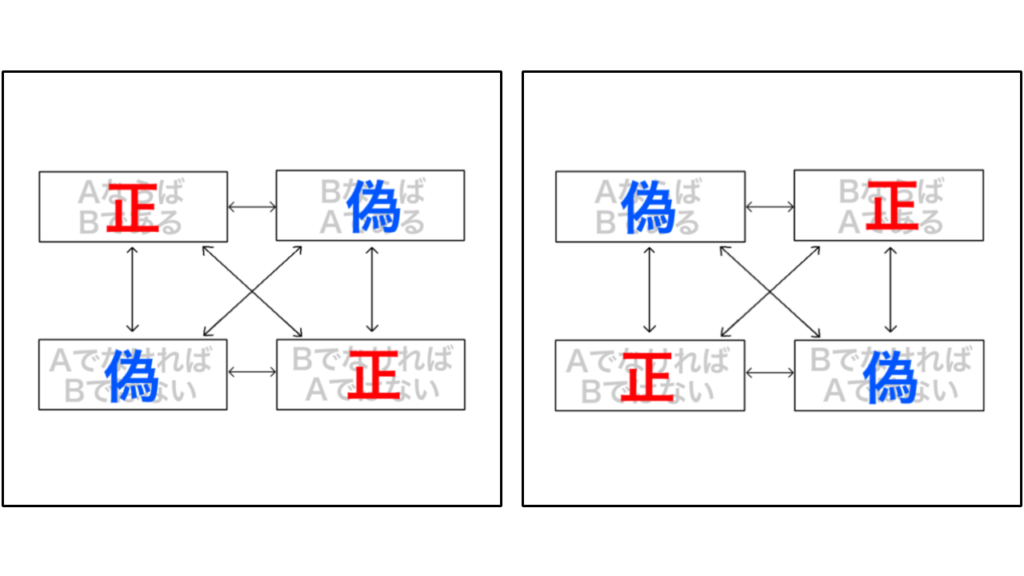
ある命題とその対偶の「正」か「偽」は必ず一致します。
命題の正か偽を証明する方法が「対偶論法」であり、対偶論法を使えばカラスを調べずに「全てのカラスは黒い」と証明できる。
と言う理論を唱えたのがヘンペルだったのです。
なるほど〜でも、そんな上手くいくんですかね？
対偶論法を使った「全てのカラスは黒い」
では、ここから本題に入ります。
パラバース博士先ほど説明したように「全てのカラスは黒い」が正であるとき、その対偶である「全ての黒くないものはカラスではない」は必ず正になります。
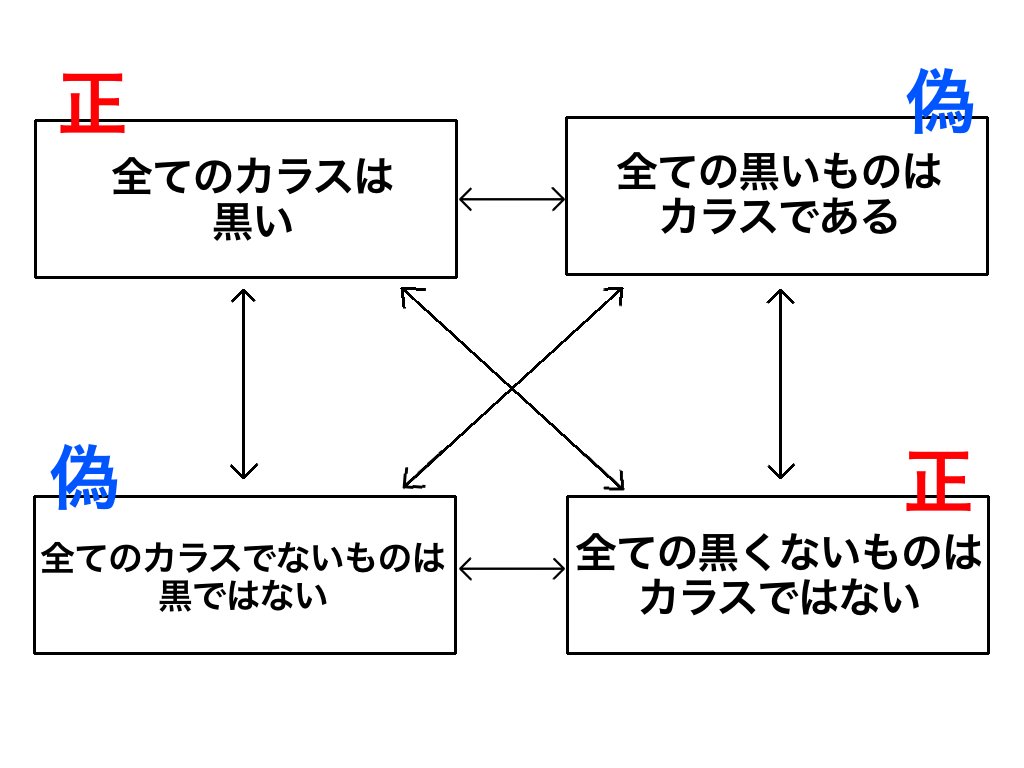
パラバース博士↑「全ての黒くないものはカラスではない」が証明できれば「全てのカラスは黒い」を証明可能です。
「全ての黒くないものはカラスではない」ことの証明方法
世界中の全ての「黒くないもの」を集めて「カラスではない」ことを確認する必要があります。
ちょっとイメージがわきません…
パラバース博士それでは、分かりやすくするために少し極端な例で考えてみましょう。
この地球上には
- 人間
- りんご
- 黒猫
- 木
- カラス
しか存在しないとします。
「全ての黒くないものはカラスではない」を証明するには、黒くないもの、つまり人間、りんご、木を全て観察して、カラスではないことを確認すればいいのです。
そうすると残りの黒い物の中にカラスがいることが分かります。
カラスを観察しなくても、人間・りんご・木を観察してカラスがいないことを確認すれば、残りのものは全て黒いので、「全てのカラスは黒い」と証明できます。
パラバース博士結果「カラス」も「黒いもの」も調べることなく「全てのカラスが黒い」ことが証明できるのです。
なるほど。理屈はわかりました！
「ヘンペルのカラス」にはなぜ違和感があるのか？
ヘンペルのカラスの謎が解けても変な感じがします？黒いものも調べずにカラスが黒いことを証明できるなんて…
パラバース博士実はヘンペルも、この違和感を伝えるためにこの問題を提唱したのです。
この違和感の正体って、何なんでしょう？
・調べなければいけないものが多すぎる、つまり現実味がない
・カラスを確認せずにカラスが黒いことを証明できてしまう矛盾感
正しいけれど矛盾しているように思えたり、間違っているように感じるものを「疑似パラドックス」といいます。
「ヘンペルのカラス」の落とし穴
パラバース博士火星人は8本足である。これは「正」と「偽」どちらでしょうか？
火星人を見たことがないので分かりません…
パラバース博士そうですね。これは「正」と「偽」どちらにも当てはまりません。
パラバース博士ですが、対偶論法を使うと、宇宙に存在する8本足でないものをすべて調べて、火星人がいなければ「火星人は8本足である」と証明することができてしまいます。
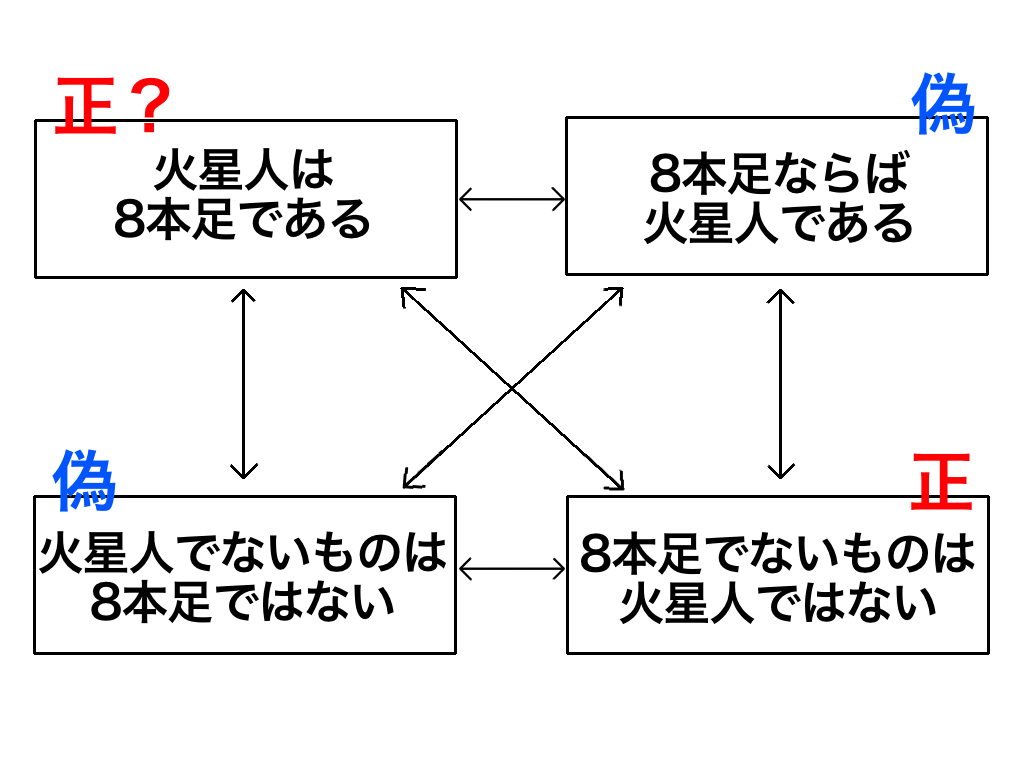
あれ？本当だ…じゃあ、対偶論法ってそもそも間違いだったんですか？
パラバース博士いえ、そうではありません。対偶論法は100％成立しうるものにしか適用できないのです。
「命題」とは、正か偽かが必ず決まる事柄です。
数学的な、例えば「2で割り切れるならば偶数である(正)」「7は10より大きい(偽)」は必ず正か偽のどちらかなので、命題であり、対偶論法を使うことができます。
対して「火星人が８本足である」は「正」「偽」どちらでもないので、命題ではなく、対偶論法も使えないのです。
パラバース博士カラスについても、黒いものもいれば灰色がかったものもいるので、そもそも「カラスは黒い」が正か偽で決定できない、つまり命題でないと主張する意見もあります。
なるほど！曖昧なものに対偶論法は使えないのですね。
実は「白いカラス」もいる
少し補足をすると、実は「全てのカラスは黒い」というのは間違っています。
というのも、アルビノと言う変種が実在しているからであり、決して「カラスの全ての個体が黒い」訳ではないからです。
まとめ
あらゆることが厳密に定義されている数学の世界においても、矛盾が生じているように感じられる。
それが、ヘンペルのカラスの面白いところです。
人間の直感というのが、いかに曖昧で信用のならないものなのかがよく分かりますね。
パラバース博士その通りです。それが人間の弱みでもありますが、それと同時に面白いところでもあると思いませんか？
コメント