今回は「パラドックスとは何か?」についてお話します。
誰もが聞いたことのある「パラドックス」。
ですが、パラドックスについて説明できる人はそういないのではないかと思います。
そして、パラドックスに似た疑似パラドックスとは?
 パラバース博士
パラバース博士この記事では、パラドックスの定義からパラドックスの例まで、知識0からでも理解できるよう解説します。
パラドックスと疑似パラドックスの違いとは?





パラドックスと疑似パラドックスってどう違うのでしょうか?



大きな違いは、前提と推察が正しいかどうかです。
| パラドックス | 疑似パラドックス | |
| 前提 | 正しそうに見える (一部に誤りがある) | 正しい |
| 推察 | 妥当に思える (誤りがある) | 正しい |
| 結論 | 受け入れがたい | 正しいが違和感がある |
パラドックスは、前提や推察に誤りがあるのに対して、疑似パラドックスにはどこにも誤りがありません。
ただし、パラドックスと疑似パラドックスの定義は明確ではありません。
疑似パラドックスを、広義のパラドックスとすることもあります。
パラドックスとは?


パラドックスとは、「正しそうな前提と、打倒に思える推論から、受け入れがたい結論が得られること」をいいます。
Paradoxという言葉はもともとはギリシア語で、para(反)+doxa(意見、通念)からきています。
日本語では背理、逆説、逆理などと言い換えられます。
パラドックスとは、例えばどういうことなのか。
有名なパラドックスの一つである「アキレスと亀」を例にあげてみます。
アキレスと亀(ゼノンのパラドックス)
アキレスという足の速い人物と、亀がいる。
アキレスと亀は徒競走をするが、アキレスのほうが早いのは明らかなため、亀がハンデをもらってかなり進んだ地点からスタートする。
スタート後、アキレスが地点Aに達した時には、亀はアキレスがそこに達するまでの時間分だけ先に進み、地点Bにいる。
アキレスが地点Bまで達すると、アキレスが地点AからBまで進んだ時間分だけ先に進み、地点Cにいる。
これを繰り返すと、アキレスはいつまでたっても亀に追いつけないことになる。





人間が亀に追いつけないなんて、ありえないですよね?でもこの説明だと確かにそうかもしれないと思えてしまいます…



このように、受け入れがたい結論が導かれる事象をパラドックスといいます。
この仮定だとアキレスは永遠に亀に追いつけないことになりますが、実際、現実ではアキレスは亀を追い抜くことができます。
つまり、この話における前提がそもそも間違っているということになります。
アキレスと亀において、なぜこのような矛盾が生じるのか、すべての人が納得できるような説明はまだなされていないそうです。
パラドックスに似た、疑似パラドックスとは?


パラドックスと似たものに、「疑似パラドックス」というものがあります。
疑似パラドックスとは、正しい仮定と正しい推論から正しい結論を導いたにもかかわらず、結論が直感に反するものを指します。
パラドックスに見えて、実はパラドックスではない、ということです。
「ヘンペルのカラス」という疑似パラドックスを例に挙げてみます。
ヘンペルのカラス
「全てのカラスが黒い」ことを証明するためには、「全ての黒くないものはカラスではない」ことを証明すればよい。
この問題では、「カラスが黒いことを、カラスを一羽も見ずに証明する方法がある」と説明されます。
カラスを一羽も見ずにカラスが黒いことを証明できるなんて矛盾しているように感じられますが、結論から言うと可能であり、論理的に正しいのです。
この、「矛盾しているように感じられるが矛盾していない」ものを、パラドックスのようでパラドックスでない、つまり「疑似パラドックス」というのです。



ヘンペルのカラスについて詳しく解説した記事もありますので、良ければご覧ください。


有名なパラドックス



有名なパラドックスと疑似パラドックスをいくつかご紹介します。
● パラドックス
- 全能のパラドックス
- 抜き打ちテストのパラドックス
- 親殺しのパラドックス
● 疑似パラドックス
- モンティホール問題
- 誕生日のパラドックス
- 消える100円玉?
パラドックス


全能のパラドックス
全能の神に不可能はない。
では、全能の神は自分が持ち上げられない重さの石を作ることはできるのか?
抜き打ちテストのパラドックス
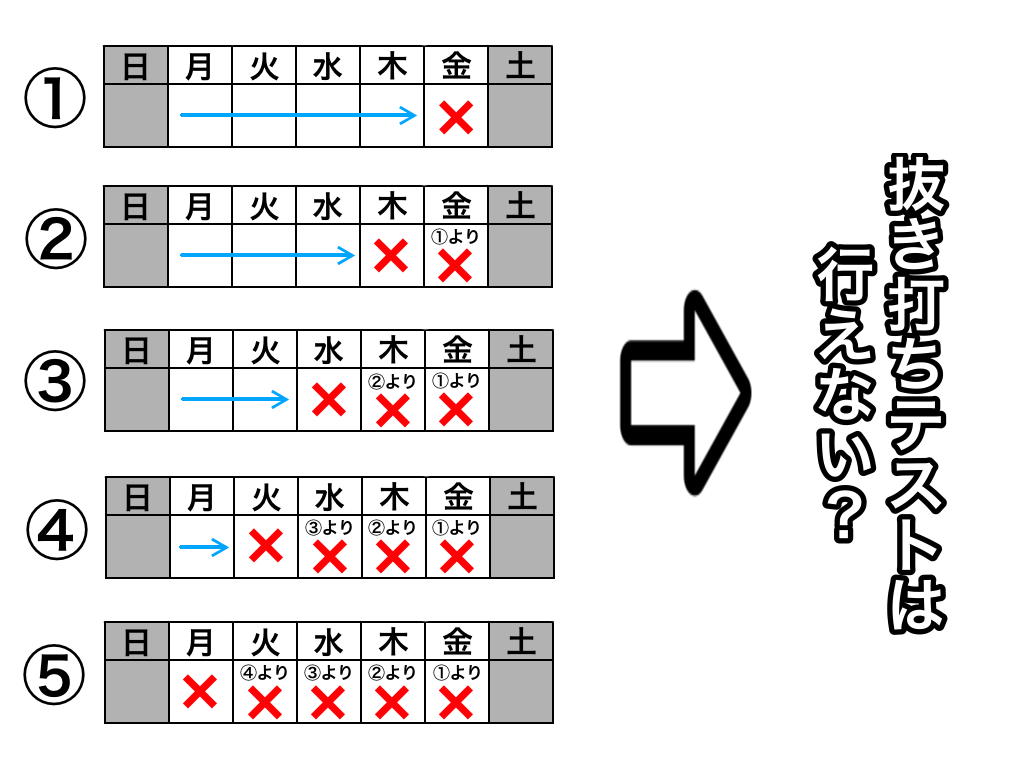
「月曜から金曜の間で抜き打ちテストをする」という予告があった。
①金曜日に抜き打ちテストが行われるとすると月曜から木曜の間にテストは行われず、金曜にテストが行われることが分かってしまうのでこれは抜き打ちテストとは呼べない。
②木曜日に抜き打ちテストが行われるとすると、月曜日から水曜日にはテストが行われず、そして金曜日に行われるテストは抜き打ちテストではないので木曜日にテストが行われることが分かってしまう。つまりこれも抜き打ちテストとは呼べない。
これを繰り返していくと、③水曜、④火曜、⑤月曜にも抜き打ちテストは行えないことになる。
つまり、「抜き打ちテストは行えない」という結論になってしまう。

親殺しのパラドックス
タイムマシンで過去に行き、自分が生まれる前に親を殺すと、自分は生まれてこないことになる。
自分が生まれなかった場合、親は殺されない。
親が殺されないのなら自分は生まれてくることになる、という循環ができる。
疑似パラドックス


モンティホール問題
回答者の前には3枚の閉じたドアがある。
1枚の扉の向こうには景品の新車が、2枚の扉の向こうにははずれを意味するヤギがいる。
回答者が扉を選ぶと司会者が残った2枚の扉のうち1枚の扉を開けてヤギを見せ、「今なら扉を変えてもいい」と言う。
回答者はここで扉を変えるべきだろうか?


誕生日のパラドックス
生徒数が23人のクラスがある。このクラスに自分と同じ誕生日の人がいる確率は50%以上。
この人数のクラスが同学年に3クラスあって生徒が69人いるとすると、同じ学年に同じ誕生日の人がいる確率は99%を超える。
一年は365日あるはずなのに、23人いれば50%、69人いれば99%を超えるのは直感に反するように思える。
消える100円玉?
ある旅行客が、1部屋1泊3,000円の旅館を訪れた。
3人の旅行客は1人1,000円ずつ出し合って、合計3,000円支払った。
旅館の女将は、「3人とも学生のようだから、少し安くして2,500円にしてあげよう。お客様に500円を返しておいて」と、3人を担当している従業員に500円を渡した。
従業員は、500円では3人で分けられないからと200円をくすねて、300円を旅行客に返した。
旅行客はその300円を3人で分けて、1人900円の支払いになったね、と言った。
旅行客が支払ったのは、900円×3人分で2,700円。
お金をくすねた従業員が持っているのは200円。
合計すると2,900円だが、旅行客が最初に支払ったのは3,000円だったはず。
残りの100円はどこへ行ったのだろうか?
まとめ
パラドックスも疑似パラドックスも、答えに感じる矛盾感が肝であり、面白いところです。



この記事で挙げた以外にもパラドックスはあるので、自分のお気に入りのパラドックスを探してみてはいかがでしょうか。