なぜ、夜空は「暗い」のか？
「太陽が沈むから」と言ってしまえばそれまでですが、
19〜20世紀まで、太陽が沈んで夜が暗くなるのは天文学的にあり得ないと考えられていました。
つまり、太陽の存在関係なく「昼は明るい」「夜も明るい」状態でないと説明が付かない。
この理論or矛盾をオルバースのパラドックスと呼びます。
「夜が暗いのはおかしい」と唱えるオルバースのパラドックスとはなにか？
パラバース博士今回は、数百年間に渡って天文学者を悩ませた「オルバースのパラドックス」を分かりやすく解説します。
パラドックスとは？
正しいそうな話が間違っていて、受け入れ難い真実がある。
もしくは、間違っていそうで間違っていない、受け入れ難い真実がある。
などをパラドックスと呼びます。
オルバースのパラドックスの概要
オルバースのパラドックスとは？
宇宙が無限大に広がっているとしたら、光り輝く星(恒星)も無限大に存在する事になります。
そして、光り輝く星が無限大にあるのならば、どの方向を見ても星の光が届くので、夜空は昼間同様に明るいはず。
しかし、現実の夜空はとても暗く、明るいとは言えません。
存在しないはずの「暗い夜空」が存在している現実との矛盾。
パラバース博士以上が、オルバースのパラドックスです。
宇宙の大きさってどれぐらい？
正確な大きさは分かっていませんが、人間からすると宇宙は無限大レベルに広いと思って下さい。
宇宙の広さが分かる例として
- 太陽以外で、地球から最も近い恒星までの距離は約39.7兆km
- 銀河系の直径は約10垓km
- 観測可能な宇宙の質量(重さ)は約4恒河沙4000極kg
↑訳の分からない数字が表記されていますが、とりあえず宇宙は果てしなく広いのです。
パラバース博士無限大レベルに光輝く星が存在するならば、夜空と宇宙は明るいはずなのです。
単純に、遠くの星は暗くて見えないから夜空は暗いのではないのでしょうか？
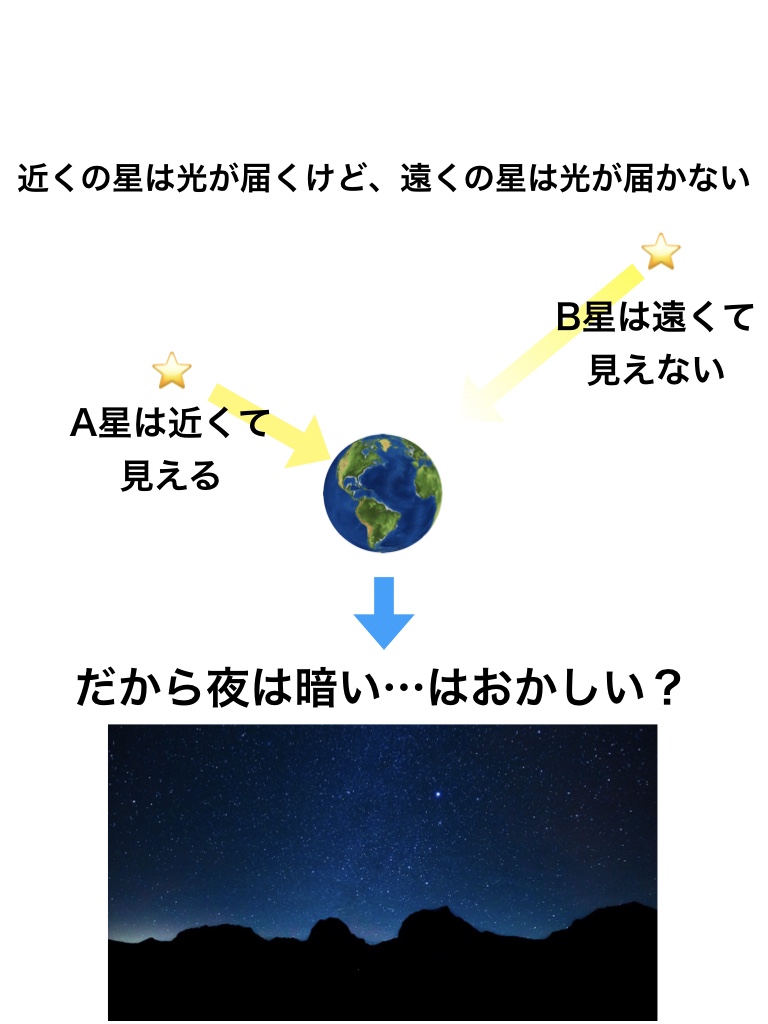
パラバース博士直感的にそう思ってしまいますが「遠くの星は暗くて見えない」はおかしな理論なのです。
遠くにある星も明るく見える？
まず、地球の周りを線引きしていくつかにグループ分けをします。
- Aグループ「100光年先」
- Bグループ「200光年先」
- Cグループ「300光年先」
パラバース博士↑A、B、Cどのグループが一番明るく見えると思いますか？
地球から一番近い「Aグループ」が一番明るく見えると思いますけど…
パラバース博士そう思いますよね。実は、A、B、Cグループの見かけの明るさは同じなのです。
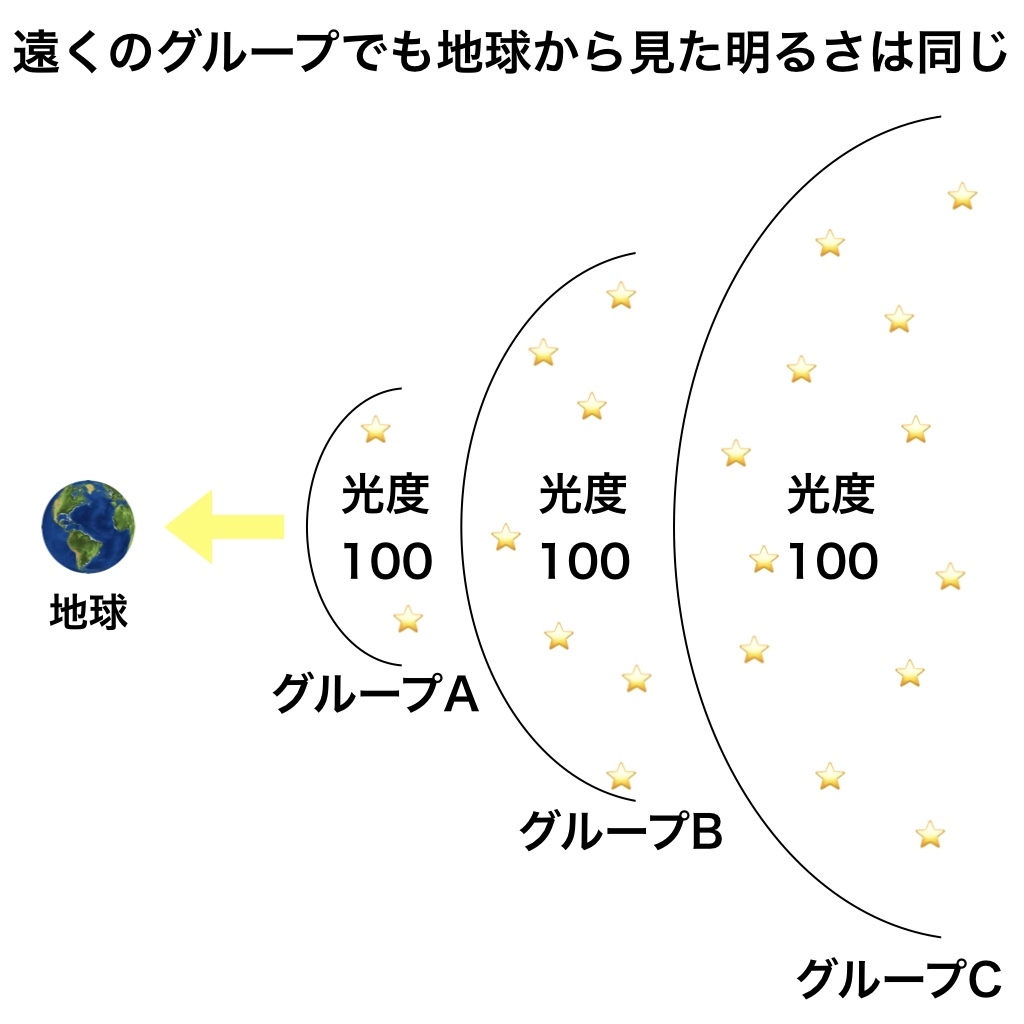
なぜ、B、Cグループは遠くにあるのに、Aグループと同じ明るさなんですか？
パラバース博士それは、遠くになるほど視野も広くなり、見える星の数も多くなるからです。
遠いグループほど星の数が多くなる
地球から100光年の距離にある星が200光年の位置に遠ざかれば、見かけの面積と明るさは1/4になります。
しかし星の数に関しては、100光年先の星の数と比べると、200光年先の星の数は4倍になります。
さらに、300光年先の星の数は100光年先に比べて9倍まで増えます。
つまり、距離が遠くになっても星の数が倍増しているから明るさも同じって事ですね？
パラバース博士その通りです。結果「遠くの星は暗くて見えない」はあり得ないのです。
小さくても沢山集まると大きな光になる
でも、いまいち「遠くの星でも沢山集まれば明るくなる」が想像できませんね💦
パラバース博士確かにそうですよね。では、例として以下の画像をご覧下さい。
宇宙から見た夜の東アジア
光り輝いている部分は「照明の光」です。
パラバース博士↑この宇宙から日本を見た場合、あなたの家の照明を見る事はできますか？
望遠鏡などは使わず、視力は1.0〜2.0ぐらいとします。
いえ、さすがに宇宙からだと私が住んでいる家の照明は見えません。
パラバース博士では、あなたが住んでいる家の照明は、写真の明るい部分と無関係だと思いますか？
無関係ではありませんよね？だって、私たちの家の照明1つ1つが集まって明るく見えている訳ですから。
パラバース博士その通り！これが「遠くの星でも沢山集まれば明るくなる」と同じ理屈なのです。
「遠い&小さいから見えない」はあり得ない
どんな小さな光だとしても、集合体となれば大きな塊となり人間の目で観測ができる様になるのです。
実際、人間を含め「物体」は全て目に見えない原子で構成されていますが、人間はその原子の集合体だからこそ目で見て確認できているのです。
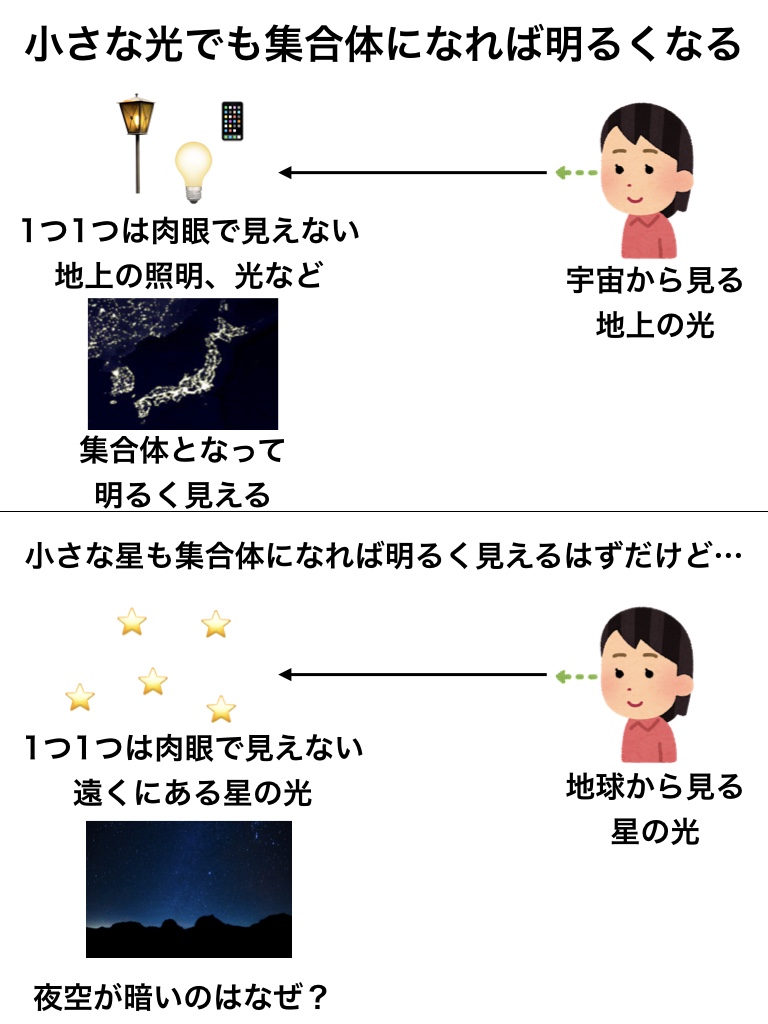
宇宙から見た東アジアの暗い部分は「人が住んでない」「光が少なすぎる」と言う絶対的な理由が存在します。
しかし、無限大レベルに広がる宇宙だと、特定の場所が暗い事はありえず、夜空に星が埋め尽くしていないとおかしいことになってしまうのです。
星が見えない「隙間」は存在しない？
あの、そもそも暗い部分には星が存在しないのではないでしょうか？
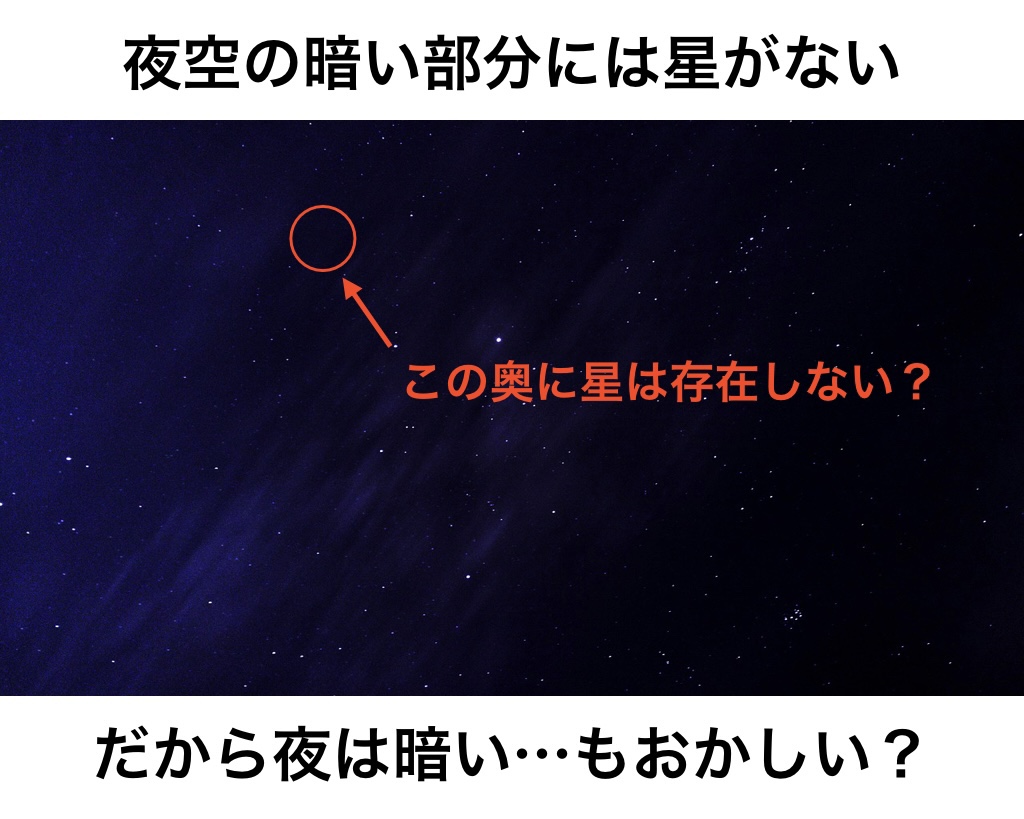
パラバース博士いえ、宇宙の広大さを考えると「暗い部分の奥に星がない」もあり得ません。
宇宙を「森」に例えると
「宇宙＝森」「光り輝く星＝木」だとします。
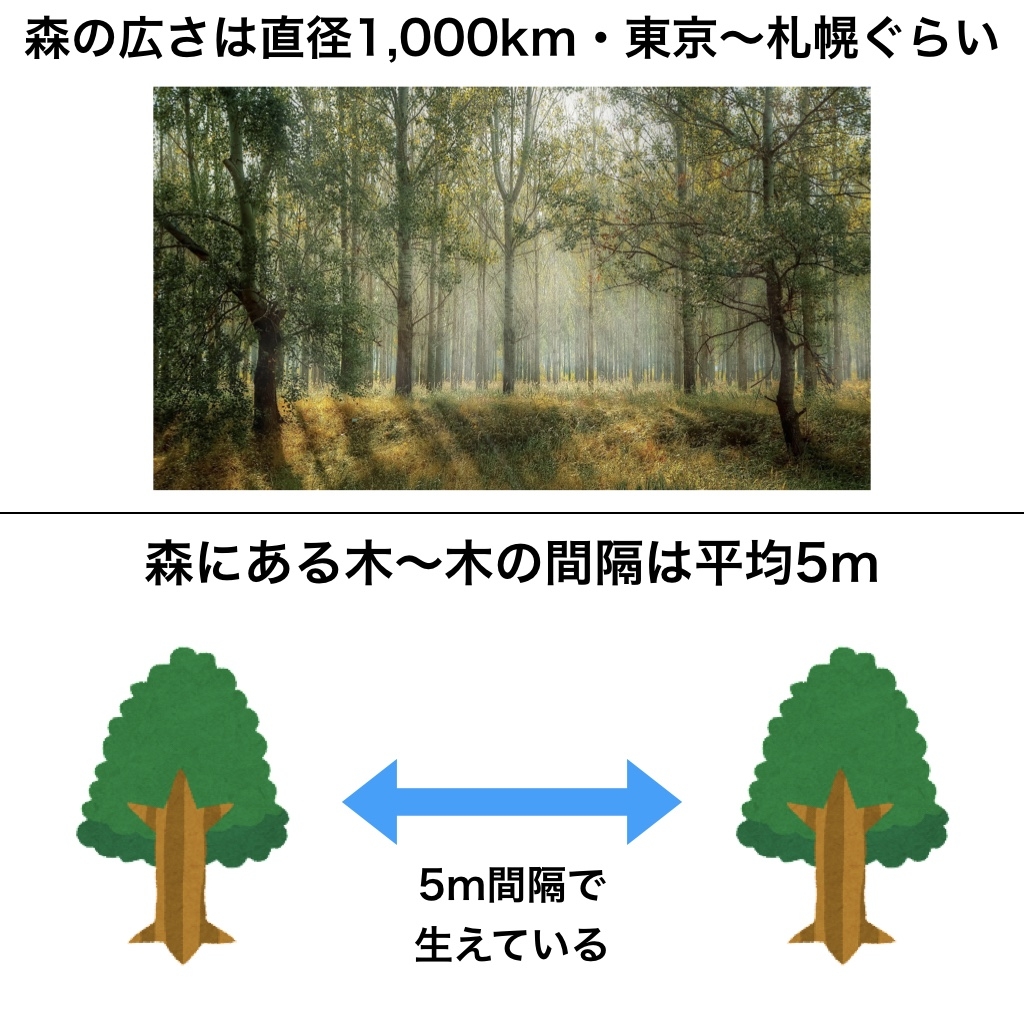
- 森の広さは直径1,000km
- 木と木の間隔は5m前後
そして、森の中いる人がダーツを真横に投げます。
投げたダーツは重力の影響を受けずに、何かに当たるまで真横に進んで行くものとします。
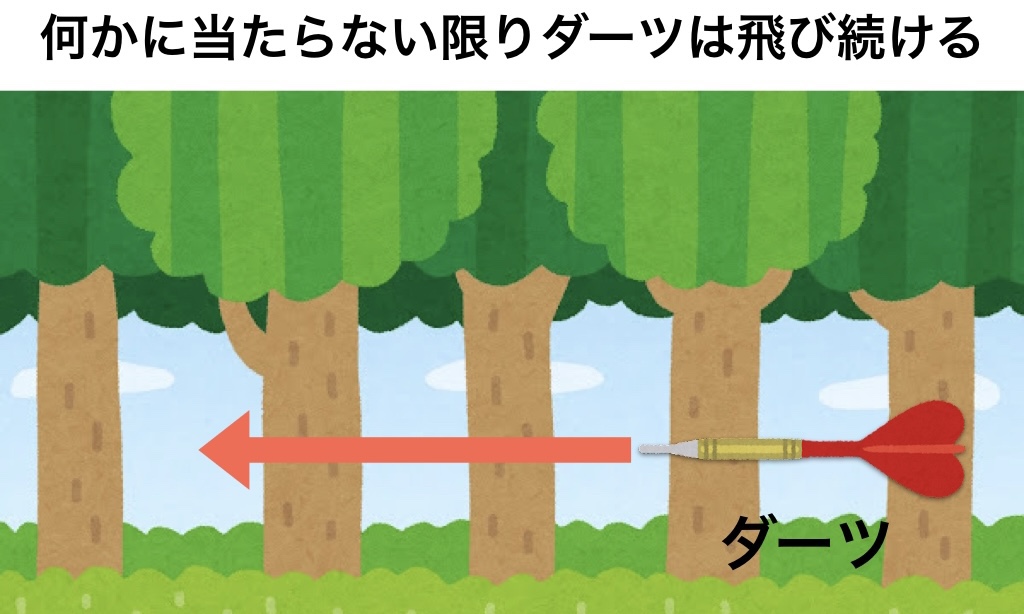
パラバース博士↑では、投げたダーツが木と木の間を潜り抜けて、森の中を抜ける事は可能だと思いますか？
いえ、投げたダーツはいつか木に当たるはずです。
パラバース博士それはなぜでしょうか？
直径1,000kmの広大な森だったら、確率的にダーツが木に当たらない事はあり得ないからです。
森が広大であれば確率的にあり得ない
森の広さが25mプールほどであれば、ダーツは木に当たらず森を抜ける事ができるかもしれません。
しかし、例題の「森」は直径1,000kmもあるので、確率的にダーツが木に当たらずに森を抜けることなどあり得ないのです。
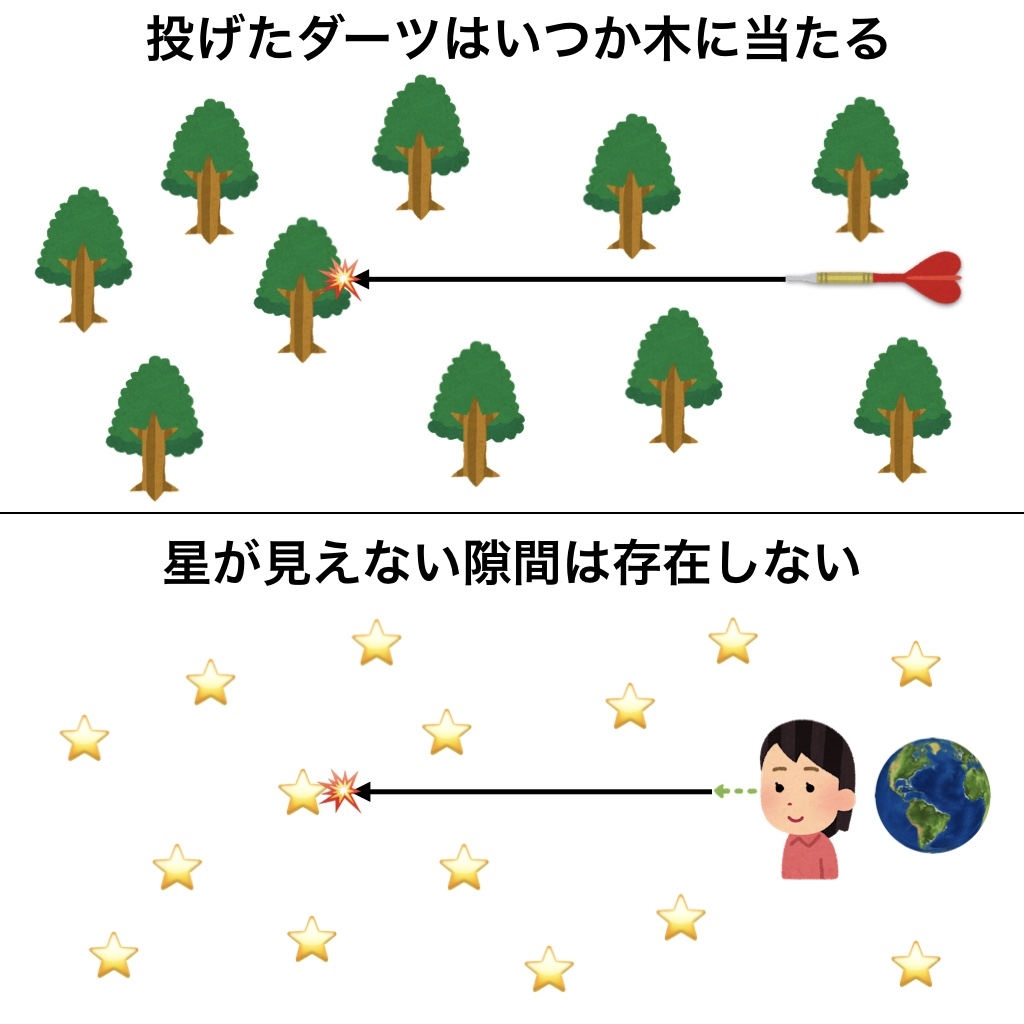
同様に、宇宙が無限大レベルに広がっているのならば、夜空の暗い部分の奥に星が存在しない「隙間」は、確率的に存在しません。
パラバース博士↑結果「暗い部分の奥に星がない」はあり得ないのです。
オルバースのパラドックスの答えを知るために！
オルバースのパラドックスの理屈は分かりましたけど…現実問題、夜空が暗いのはなぜでしょうか？
パラバース博士ではここから、オルバースのパラドックスの答えを知るために絶対覚えておくべきポイントを解説します。
星の光が地球に届くまでタイムラグがある
太陽や月の光を含めて、星の光が地球に届くまでに一定の時間がかかる事が分かっています。
そして、光が届くスピードは遠くにある星ほど時間がかかります。
恒星の光が地球に届くまでの時間の例
- 太陽の光が地球に届くまで約8分19秒
- シリウスの光が地球に届くまで約8.6年
- カシオペヤ座V762の光が地球に届くまで約1万6000年
「光年」とは光が1年間に進む距離の事で、1光年は約9兆5000億kmに及びます。
パラバース博士単純計算で、今夜空に輝いているカシオペヤ座V762の光は約1万6000年前に輝いていた光なのです。
そう考えるとすごいですね。
遠くの星の光が届くまで時間がかかる
例題、宇宙が「有限」で「今」誕生したとしたら？
宇宙の広さが半径100光年までの有限だとします。
そして、地球は今この瞬間に誕生したとします。
地球が生まれた年数は「0」の状態。
- 1光年先にある「A星」
- 10光年先にある「B星」
- 100光年先にある「C星」
パラバース博士↑上記3つの星が地球に届くまでどれぐらいかかると思いますか？
「A星＝1年」「B星＝10年」「C星＝100年」ですよね？
パラバース博士↑上記の3つの星だけで夜は明るくなると思いますか？
いえ、3つの星の光だけでは夜空が明るくならないと思います。
夜空が明るくするには時間がかかる
星の光が時間差で地球に届くのであれば、遠くの星ほど長い年月をかけて地球に届く事になります。
今の夜空が星で満たされて明るかったとしても、遠くの星の光が届く前、大昔の夜空は暗かった事ですね？
パラバース博士その通りです。以上の事を踏まえて、何km先までの星が見えれば夜空が明るくなるのか？を解説します。
何km先の星が見えると夜空が明るくなる？
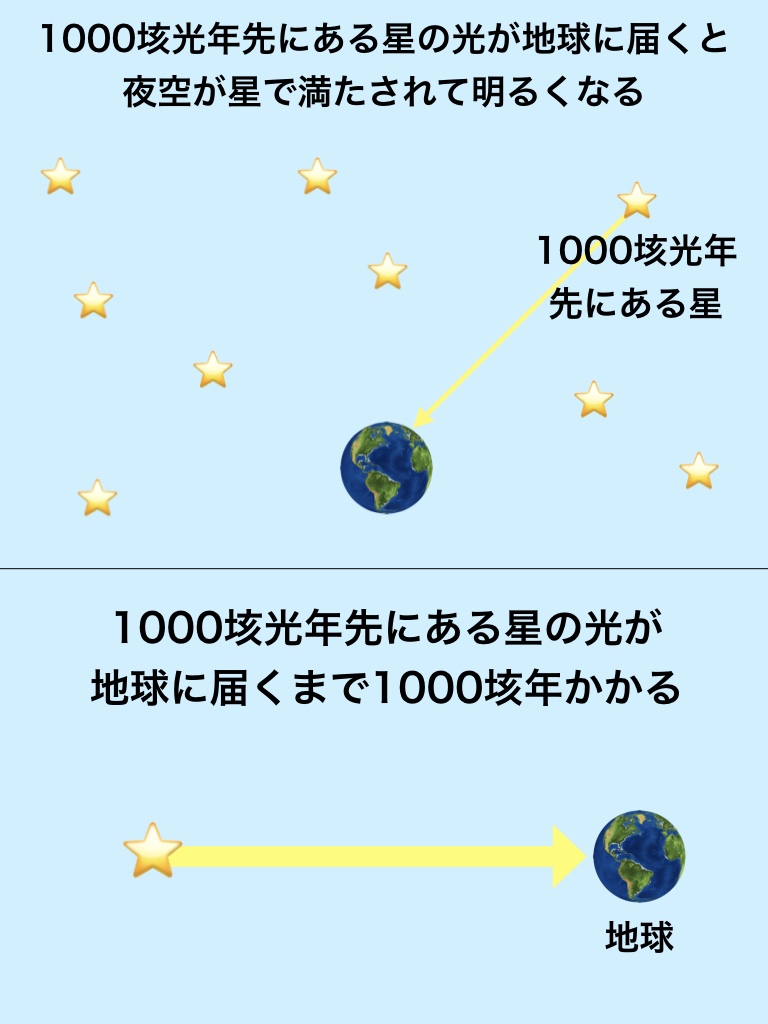
夜空が星で埋め尽くして明るくなるには？
星同士の間隔を計算に入れた上で、どれぐらい先の星まで見えてば夜空が明るくなるのか？
導きだされた答えは
パラバース博士「1,000垓光年」先までの星が見えると、夜空が明るくなります。
一・十・百・千・万・億・兆・京・垓
1,000垓って…普段使用しない桁だからピンとこないです💦
1000垓光年を「km」で換算すると？
1000垓×9.5兆
100,000,000,000,000,000,000,000×9,500,000,000,000＝1×9.5の35乗なので
1000垓光年＝約950,000,000,000,000,000,000,000,000,000,000,000 kmです。
漢数字で表すと約9,500溝(こう)km
現在の宇宙年齢は約138億年
パラバース博士実は、宇宙は誕生してから138億年しか経っていません。
え？138億年だと1,000垓光年の星の先が全然届きませんよね。
1,000垓−138億＝999垓9999京9999兆9862億光年なので
夜空が星で明るくなるには、あと999垓9999京9999兆9862億光年分の星の明るさが必要になるのです。
138億光年分の星の光では、夜空でも明るくするために必要な光度の1%にも満たない数字。
- 100,000,000,000,000,000,000,000(1,000垓)
- 13,800,000,000(138億)
↑桁数を並べて分かる通り、全く足りません。
計算式の注意点
巨大な数字を四捨五入して計算しているため、数億～数百兆レベルの誤差があると思って下さい。
オルバースのパラドックスの答え
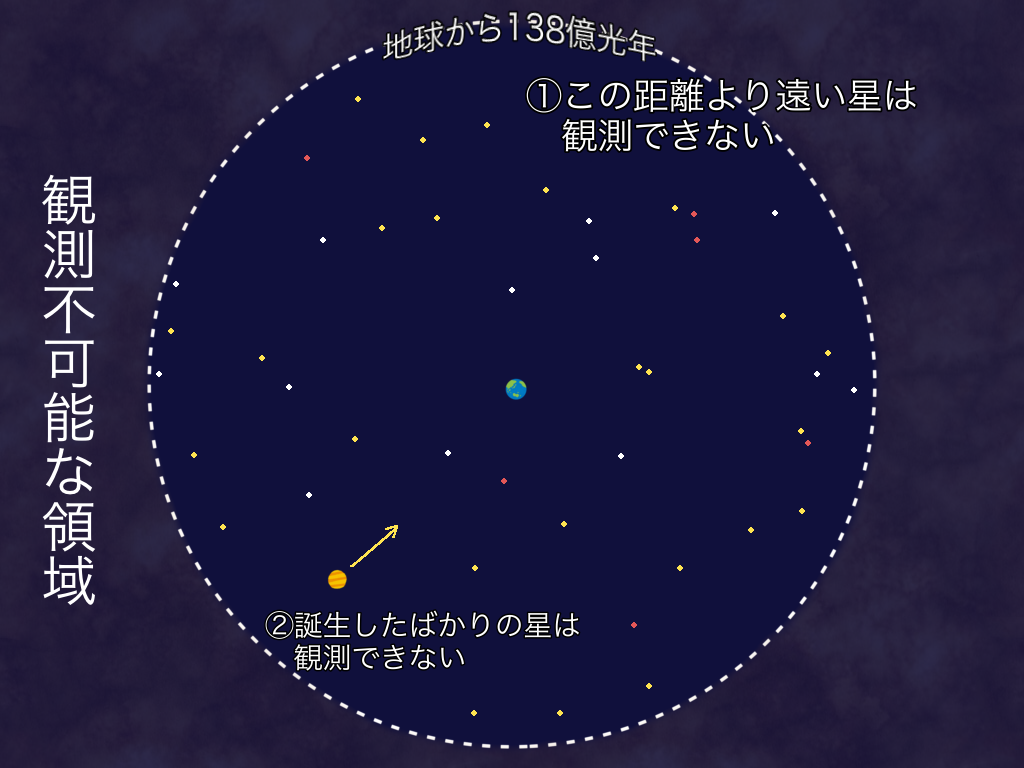
オルバースのパラドックスの答え合わせ
夜空を明るくするには、約1,000垓光年先の星まで見える必要がある。
約1,000垓光年先の星は、約1,000垓年経たない見る事ができない。
宇宙は誕生してから約138億年しか経ってないので、約1,000垓光年先の星の光が地球に届いていない。
結果、約138億年分の星の光で夜空は明るくならないので、地球の夜空は暗い。
パラバース博士↑これが、オルバースのパラドックスの結論になります。
なるほど！地球にはまだ「光が届いてない」と言うのが答えなんですね。
オルバースのパラドックスって、天文学的な数字が出てくる壮大な話でしたけど、納得できる答えだと思います。
パラバース博士ありがとうございます。ただ、1つだけ注意点があります。
138億光年先は誤り？
宇宙が誕生してから138億年なので、地球から見える星は138億光年先までだと思いますが、厳密に言うとこれは誤りです。
なぜなら、宇宙は膨張していると考えられているので、宇宙の膨張を計算に入れて地球から見える星の限界値は、約464億光年先になるのです。
ただ、計算と説明がややこしくなるので本記事では約138億年にしています。
夜空が明るくなる事は永遠にない？
とてつもなく未来の話になりますが、今から999垓9999京9999兆9862億年後の夜は明るくなっているんですかね？
(宇宙の膨張は計算に入れていません)
パラバース博士単純計算するとそうなりますが、残念ながらそれはないと思われます。
宇宙の余命は後1400億年？
宇宙には始まりもあれば「終わり」もあります。
諸説ありますが、宇宙の余命は約1,400億年と考えられています。
当然、約1,400億年では1,000垓年には遠く及ばないので、夜空が明るくなる前に宇宙は寿命を迎えてしまうのです。
宇宙に寿命なんてあったんですね…
パラバース博士さらに言うと、太陽にも寿命があるのでその観点でも、1,000垓年待つのは不可能です。
その前に地球が滅びる？
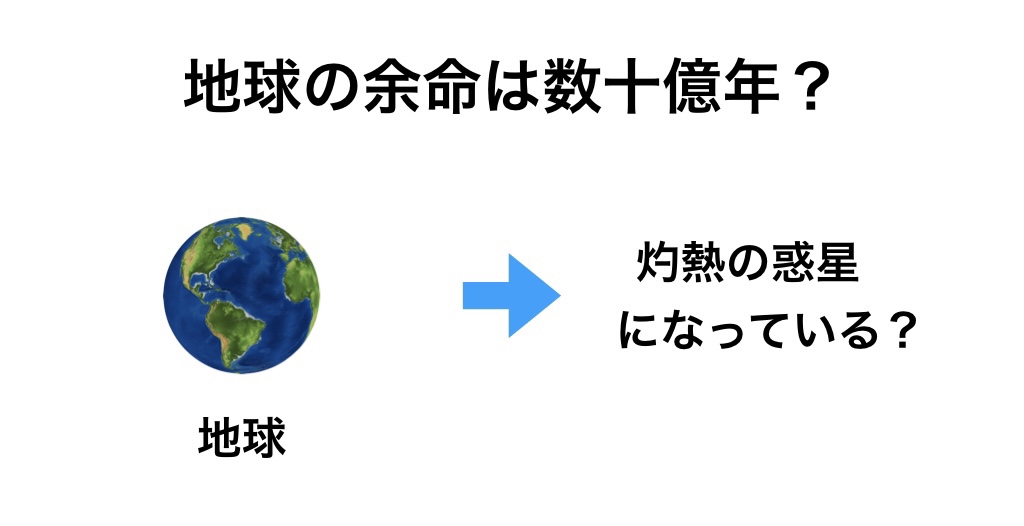
宇宙の余命以前に、地球は後10億年もすると太陽の膨張で表面温度が上がり海が蒸発。
40億年後は、さらに表面温度が上がり生命が住めない惑星に。
70億年後になると太陽が地球の軌道近くまで接近して、灼熱の惑星になっていると考えられています。
当然、この様な環境下では人間が住む事は出来ません。
70億年も果てしなく未来の話ですけど…1,000垓年と比べるとあっと言う間に感じちゃいます💦
パラバース博士この頃人類は他の惑星に移住しているのか？とっくに滅んでいるのか？それは、未来だけが知る事実です。
オルバースが唱えた仮説とは？
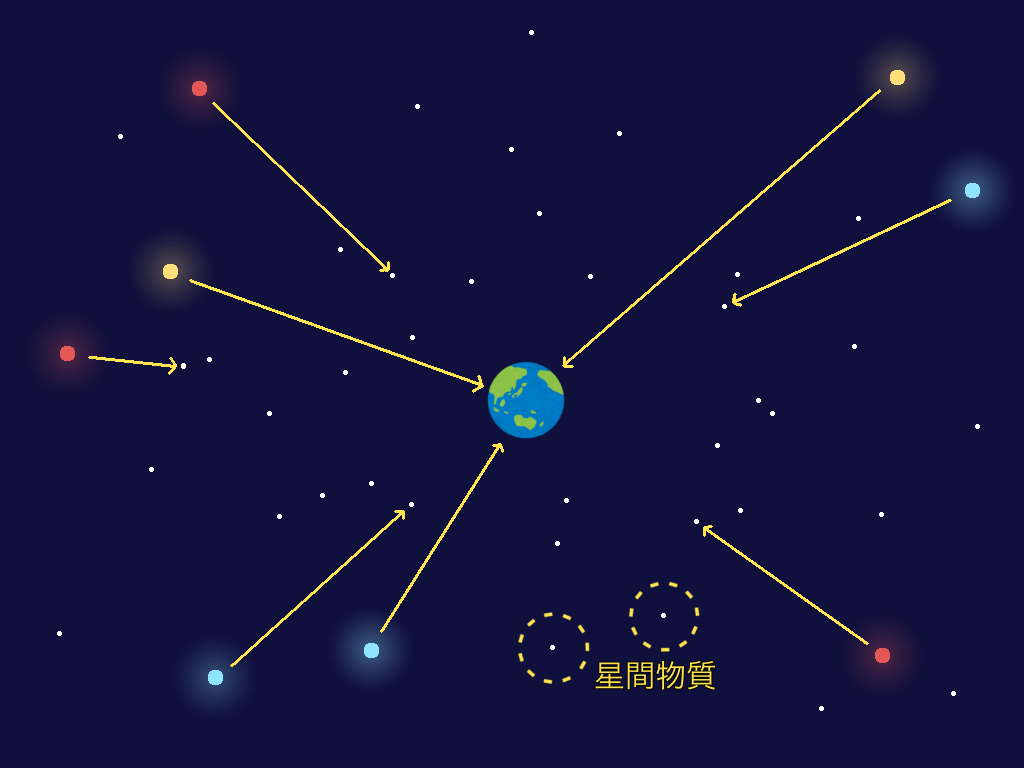
パラバース博士最後に、オルバースのパラドックスの謎を解決しようとした先人の仮説をご紹介します。
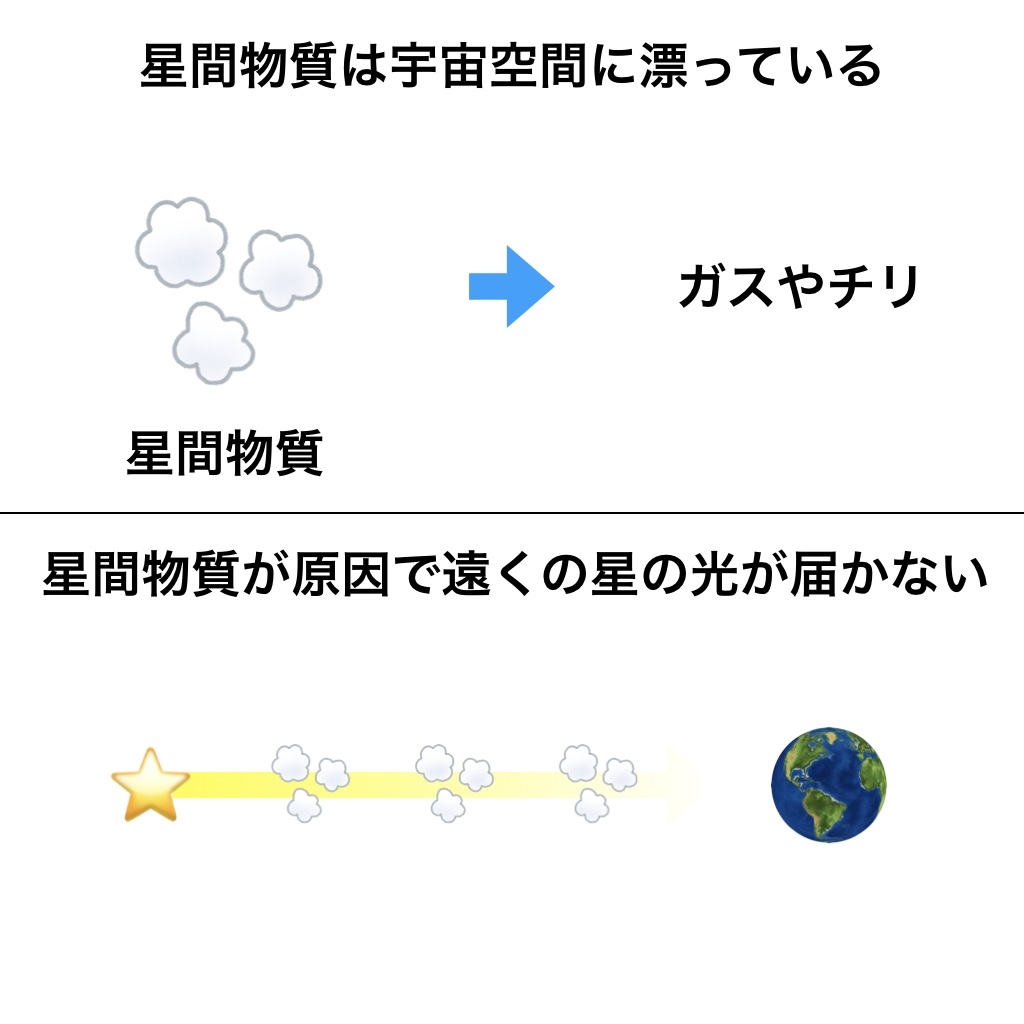
「星間物質」が星を隠している説
星間物質(せいかんぶっしつ)とは、宇宙空間い漂うチリやガスの事で、例えるなら霧(きり)の様な存在です。
地球で霧が発生すると、遠くまで見る事ができず、近くの物しか見えなくなってしまいます。
オルバースのパラドックスでも、星間物質が邪魔をして遠くの星を隠してしまうので、遠くの星を見る事が出来ない。
結果、近くの星だけ光り輝いているのではないか？と言う仮説です。
パラバース博士ちなみに、この仮説を唱えたのが「ヴィルヘルム・オルバース」です。
あ、オルバースのパラドックスってその人の名前が由来なんですね？
でも、星間物質の仮説は間違っていた
ヴィルヘルム・オルバースが唱えた星間物質によって星が見えない仮説は間違っていました。
なぜなら、宇宙空間に漂う星間物質は星の光を隠すほど沢山存在せず、ごく少量だったからです。
また、もし星を隠せるほどの星間物質が存在したとしても、星間物質が恒星の光と熱を浴びると、恒星と同じレベルの光と熱を発してしまいます。
そのため、星間物質が星を隠していても、夜空は明るくなるのです。
星間物質の仮説が否定されると、その後しばらくオルバースのパラドックスは謎に包まれた状態になります。
その後の成り行き
アインシュタインによる一般相対性理論の発表。
エドウィン・ハッブルによって「宇宙が膨張している」事が明らかになると、オルバースのパラドックスは徐々に解明されて行くことになります。
パラバース博士そして現在「地球にはまだ光が届いてない」と言う結論が導き出されたのです。
まとめ
もし、夜空が明るかったらどんな世界になってたんですかね？
パラバース博士昼と夜の繰り返しは、生命が育む上で重要なプロセス(工程)なので、地球上の生態系は大きく変わっていたかもしれません。
パラバース博士もしかしたら、夜が存在しない事で人類が誕生しなかった可能性だってあります。
パラバース博士この記事を最後まで読んでくれた方へ。夜が明るかったらどんな世界になっているか？想像してみてほしいです。
コメント